機械学習で株価変動を予測してみる(2)~最初の失敗
try1: 前回の訓練結果の考察
テストデータでの予測精度98%って良すぎますね!
まずは、訓練データとテストデータで、UP/EVEN/DOWNの分布がどうなっているか調べよう
今回用いた株価データは、2015年1月26日~2020年2月7日のSUBARU(証券コード:7270)です。まず、全ての日の終値と前日の終値からの変動率を算出します。ある日の終値C[D]の変動率ROC[D]は前日(D-1)の終値C[D-1]から以下の式で算出できます。
ROC[D] = C[D] / C[D-1] * 100
そして以下の3種類に分けます。
- UP: 着目日の終値が前日の終値より3%以上上昇した
- DOWN: 着目日の終値が前日の終値より3%以上下落した
- EVEN: 前日終値からの変動が±3%未満
すると、それぞれ日数と比率は以下のようになりました。
| 変動率3% | up | up(%) | even | even(%) | down | down(%) | total |
| 1日後 | 76 | 5.9 | 1138 | 88.7 | 69 | 5.4 | 1283 |
これを、以下のように訓練データとテストデータに分けました。
- 訓練データ: 2015年1月8日~2019年8月31
- テストデータ: 2019年9月1日~2020年2月7日
すると、それぞれ日数と比率は以下のようになりました。ここで、株価の75日移動平均を算出したため、有効なデータ数は上記より74個減っています。さらに、1つの訓練データはある指標の5日分のデータとしているので、さらに4個減ります。
| 変動率3% | up | up(%) | even | even(%) | down | down(%) | total |
| 訓練データ | 51 | 5.8 | 791 | 89.4 | 43 | 4.9 | 885 |
| テストデータ | 2 | 1.9 | 102 | 98.1 | 0 | 0.0 | 104 |
あれまぁ、UP=テストデータで前日の終値より3%以上上昇した日が2日、DOWNは0日で、ほぼEVENの日ばかりとなっています。
| 変動率3% | up | up(%) | even | even(%) | down | down(%) | total | total(%) |
| 訓練正答数 | 51 | 0.0 | 791 | 100 | 0 | 0.0 | 791 | 89.9 |
| 推論正答数 | 0 | 0.0 | 102 | 100 | 0 | 0.0 | 102 | 98.1 |
で、推論結果の正答数をUP/EVEN/DOWN毎に見ると、UPが16日中0日、EVENが102日中102日、DOWNが0日中0日となっています。つまり、104日分のテストデータのうち、正答だったのはEVEBの102日分だったのですが、UP/DOWNの正答すうはとても低いことがわかります。これは、もともとEVENのデータが多いから、このように見せかけの正答率が98%と、ほぼ完ぺきな正答率になったのだと考えられます。
ここで、「UP=変動率が3%以上」「DOWN=変動率が3%以下」というのは、銘柄によっては該当する日数が少なくなる期間があるので、この判断基準を見直す必要がありそうです。で、どうするか…。この辺りが機械学習の難しさの一つだと思いますが、訓練データの量・質に応じて結果が変わります。
try2: 訓練データの見直し(UP/EVEN/DOWNを1/3ずつにする)
まず思いついたのは、
- 訓練データの分布を、UP/EVEN/DOWNが1/3ずつ出てくるようにする
です。やり方は、
- N個の日足データから各日の変動率を算出し、配列に格納
- 変動率で降順にソート(大きい値→小さい値)
- 要素番号N/3の位置の変動率をUPの基準値とし、要素番号N*2/3の位置の変動率をDOWNの基準値とする
これで、配列の0~N/3までの要素がUPの要素、N/3+1~N*2/3-1の要素がEVENの要素、N*2/3~N-1の要素がDOWNとなり、それぞれ全データ数の1/3ずつとなります。
| 変動率3% | up | up(%) | even | even(%) | down | down(%) | total |
| 訓練データ | 284 | 32.1 | 298 | 33.7 | 303 | 34.2 | 885 |
| テストデータ | 25 | 24.0 | 49 | 47.1 | 30 | 28.8 | 104 |
上のように、UP/EVEN/DOWNの個数がほぼ1/3ずつになりました。この学習データで訓練し、推論した結果が以下です。
| 変動率3% | up | up(%) | even | even(%) | down | down(%) | total | total(%) |
| 訓練正答数 | 181 | 63.7 | 199 | 66.8 | 78 | 25.7 | 458 | 51.8 |
| 推論正答数 | 25 | 24.0 | 49 | 47.1 | 30 | 28.8 | 45 | 43.3 |
訓練データでの正答率が51.8%、推論データでの正答率が43.3%となり、予想通り「あたる確率は約1/2」となり、サイコロを振ってるのと同じような確率になりました。
また、UPをDOWNと判断したり、DOWNをUPと判断するのは結構致命的な誤りだと考えられます。その回数を数えると以下の通りでした。
- 実際はDOWNだったのにUPと判断した回数は11回
- 反対にUPをDOWNと判断した回数は2回
try3: 訓練データの見直し(UP=25%/EVEN=50%/DOWN=25%にする)
うーん、UP/EVEN/DOWNを1/3ずつにするのは単純すぎるかなぁ、と思ったので、
- 訓練データの分布を、UP=25%/EVEN=50%/DOWN=25%にする
です。やり方は、上記と同様に、
- N個の日足データから各日の変動率を算出し、配列に格納
- 変動率で降順にソート(大きい値→小さい値)
- 要素番号N/4の位置の変動率をUPの基準とし、要素番号N*3/4の位置の変動率をDOWNの基準値とする
これで、配列の先頭から25%までの要素がUPの要素、末尾の25%がの要素がDOWNとなり、それ以外がEVENとなります。
| 変動率3% | up | up(%) | even | even(%) | down | down(%) | total |
| 訓練データ | 215 | 24.3 | 435 | 49.2 | 235 | 26.6 | 885 |
| テストデータ | 18 | 17.3 | 63 | 60.6 | 23 | 22.1 | 104 |
上のように、UP/EVEN/DOWNの個数がほぼ1/3ずつになりました。この学習データで訓練し、推論した結果が以下です。
| 変動率3% | up | up(%) | even | even(%) | down | down(%) | total | total(%) |
| 訓練正答数 | 106 | 49.3 | 393 | 90.3 | 12 | 5.1 | 511 | 57.7 |
| 推論正答数 | 0 | 0 | 53 | 84.1 | 1 | 4.3 | 54 | 51.9 |
訓練データでの正答率が57.7%、推論データでの正答率が51.9%となり、少し改善しました。致命的な推論ミスは、
- 実際はDOWNだったのにUPと判断した回数は3回
- 反対にUPをDOWNと判断した回数は0回
となり、こちらも改善しました。
パラメタの可視化
今回用いたNNは3つのパラメタW1,W2,W3があります。上記3通りの学習結果でそれぞれのパラメタがどのような値になったか、カラーバー表示して確かめました。
それぞれ左から順番にW1, W2, W3のパラメタを可視化したもので、値が0なら白、+2.0に近ければ濃い赤、-0.2に近ければ濃い青になります。try1~try3でパラメタの値のレンジが少し違うので、0以外の値は必ずしも同じ値が同じ色になるとは限りません。
各層のノード数とW1~W3の行列サイズは、以下の表のようになっています。
| ノード数 | |
| 入力層 | 5 |
| 中間層1 | 10 |
| 中間層2 | 10 |
| 出力層 | 3 |
| 行列サイズ | |
| W1 | 5行10列 |
| W2 | 10行10列 |
| W3 | 10行3列 |
try1のパラメタ
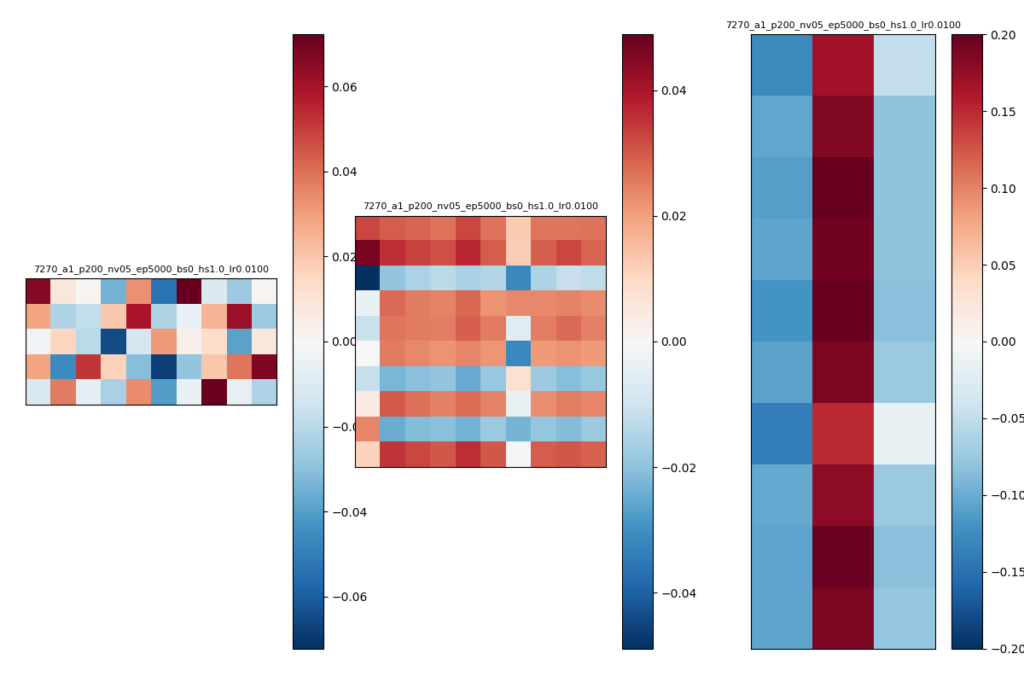
- W1はほぼ規則性は見られない
- W2は水平方向に同じような係数が並ぶ傾向
- W3は垂直方向に同じような係数が並ぶ傾向
- 推論結果ではEVENになる確率が高いが、W3の2列目(真ん中の列)がそれに対応していると考えらる
try2のパラメタ
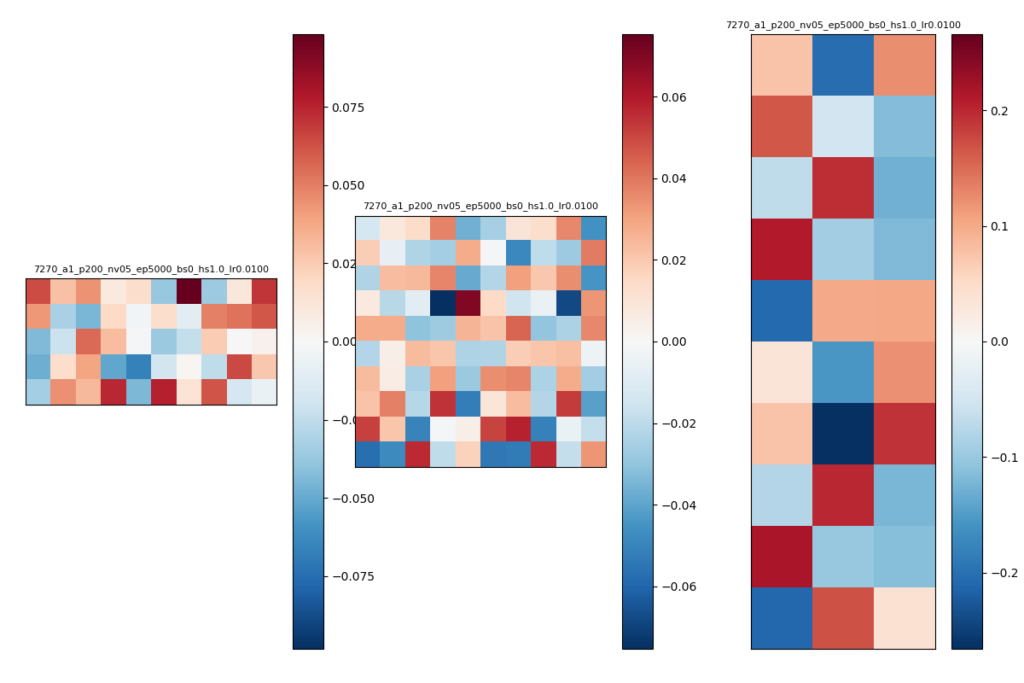
- W1~W3どれも規則性は見られない
try3のパラメタ
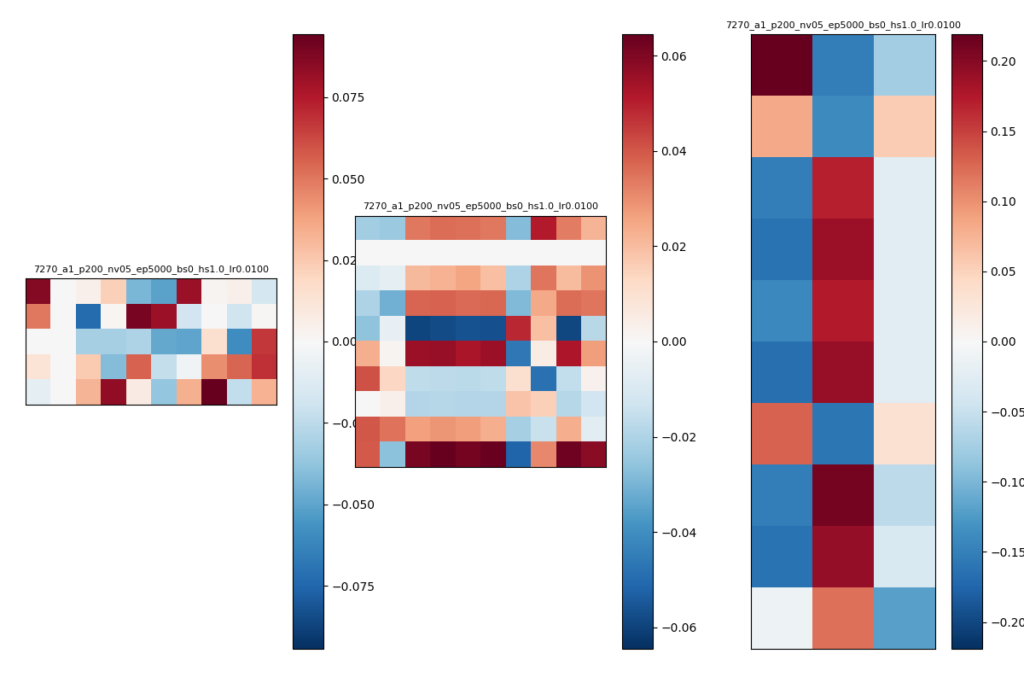
- W1の2列目とW2の2行目はすべて0に近い係数になっており、これらに関する入力データは推論結果に影響を与えないと考えらえる。
これらの結果から、try1, try3は初期値(乱数=砂嵐パタン)ではないので、それなりに学習されたと言える。それ以上のことはこの結果からは言えない。
今後の対策
訓練データでの正答率があまり高くないので、改善案としては
- 学習の回数を増やす
- [現状] EPOCH数=5000
- [改善案] EPOCH=10000, 20000, 50000, …
- 学習データの内容を変える
- [現状] 今は前日の前日終値から当日終値の変動率を5日分使って学習
- [改善案] 5日移動平均、75日移動平均の変動を見る、など
おまけ
実は上記の改善をしたのに、まだ正答率が98%でした。推論精度がよいので「おぉ、やってみたら意外と高精度で予測できてる、さっそく株を買おうか」と思ったのですが、あれこれ考えて見直しているうちに、訓練データの作り方が致命的に間違ってて、未来の情報を使って学習していたことが判明しました。そのため、テストデータの正答率98%という異常な精度が出ていたのでした・・・。早まって取引せずによかったです(汗)。


ディスカッション
コメント一覧
まだ、コメントがありません